Staggered Packing of Cylindrical Containers

Assuming the containers must touch, in one direction:

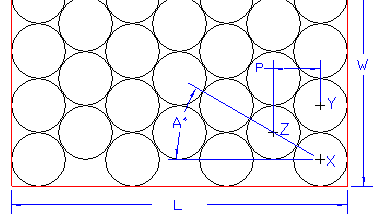
If N is the number of columns and Dia the diameter of the cylinder, then:

L = Dia + (N - 1) * P
P = Dia * COSINE A

Since XYZ is an equilateral triangle, angle XYZ must be 60 degrees and therefore, angle A = 30 degrees.

P = Dia * COSINE 30 or P = Dia * 0.866025404

Therefore: L = Dia + (N - 1) * 0.866025404 * Dia
(Obviously W would be Dia multiplied by the number of cylinders in the column)

In the calculator below enter the diameter of your cylindrical pack (Dia) and the No. of Columns (N), then click the "Calc Length Size" button to find the minimum pack length size.

Dia. :	No. of Columns (N):
P =	Length Size (L) =

Assuming staggering in both directions:

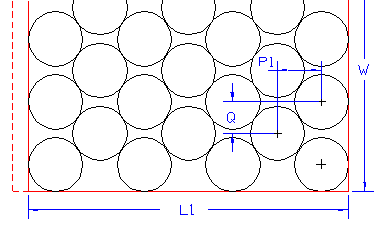
If it is necessary to reduce L (probably to improve the pallet fill), it is obvious that W will increase. To calculate the increased value of W:

Let L1 be the new value of L. Then:

L1 = Dia + (N - 1) * P1

P1 = (L1 - Dia) / (N - 1) 

Q = $\sqrt{\mathrm{(Dia²)\; -\; (<font\; color="blue">P1</font>²)}}$

Having obtained the value of Q, W may then be calculated by taking into account the number of rows (remember the rows in their columns are staggered, the illustration shows 6 rows in a Pack Width with the edge of the box cut off). Naturally, staggering should be avoided because it means that more "air" is packed, so increasing the board area used per retail pack.

In the calculator below enter the diameter of your cylindrical pack (Dia), the No. of Columns in the new Length (N), the No. of Rows in the new Width and the new Length size (L1) that you would like, then click the "Calc Width Size" button to find the minimum new pack width size.

Dia. :	No. of Columns in L1 (N):
No. of Rows in new Width  =	Length Size (L1) =
P1 =	Width Size (W) =
Q =